O(2^n) - EXPONENTIAL TIME
The Recursive Explosion - When Algorithms Go Nuclear!
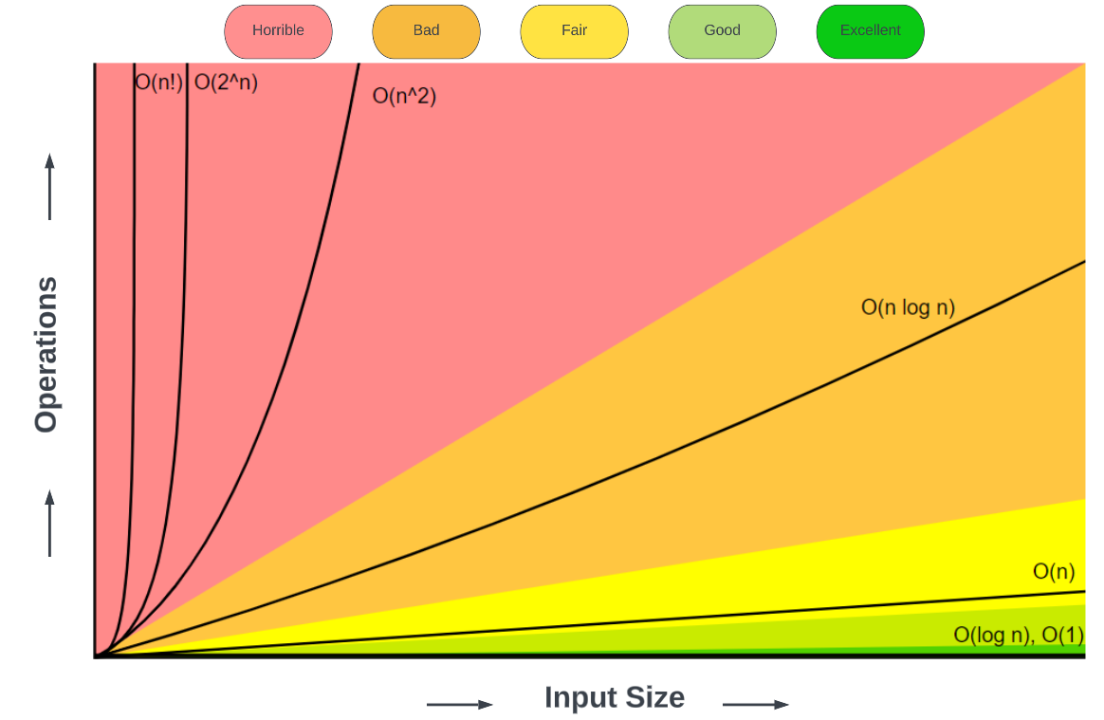
Where Are We in the Scope of Complexity?
What is O(2^n) - Exponential Time?
The Recursive Monster 💥
O(2^n) means the algorithm’s time doubles with each additional input element - creating explosive growth!
Real-World Analogy: * Like a chain letter where each person sends to 2 more people * Day 1: 1 person, Day 2: 2 people, Day 3: 4 people… * Day 30: Over 1 billion people!
Explosive Growth Pattern 🚀
- 10 items → 1,024 operations
- 20 items → 1,048,576 operations
- 30 items → 1,073,741,824 operations
- Each +1 item doubles the work!
Key Insight 🔑
The algorithm typically uses recursion where each call creates two more calls, creating an exponential explosion.
Danger Signal: “Does my recursive function call itself multiple times?”
If yes → Might be O(2^n)!
What Creates O(2^n) Complexity?
The “Branching Recursion” Pattern 🌳
O(2^n) algorithms typically involve recursive functions that branch into multiple recursive calls.
Naive Fibonacci - The Classic
def fibonacci_slow(n):
if n <= 1:
return n
# This creates the exponential explosion!
return fibonacci_slow(n-1) + fibonacci_slow(n-2)
# Why O(2^n)?
# Each call creates 2 more calls
# fibonacci_slow(5) calls:
# - fibonacci_slow(4) and fibonacci_slow(3)
# - fibonacci_slow(4) calls fibonacci_slow(3) and fibonacci_slow(2)
# - fibonacci_slow(3) calls fibonacci_slow(2) and fibonacci_slow(1)
# And so on... massive redundant work!
# The call tree grows exponentially:
# fib(5)
# / \
# fib(4) fib(3)
# / \ / \
# fib(3) fib(2) fib(2) fib(1)
# ...and it keeps branching!Subset Generation
def generate_subsets(items):
if not items:
return [[]] # Base case: empty set has one subset
# For each subset of remaining items,
# create two versions: with and without first item
first = items[0]
rest_subsets = generate_subsets(items[1:]) # Recursive call
# Double the subsets: add first item to each subset
with_first = [[first] + subset for subset in rest_subsets]
return rest_subsets + with_first
# Example: [1, 2, 3] has 2³ = 8 subsets:
# [], [1], [2], [3], [1,2], [1,3], [2,3], [1,2,3]
# Each element doubles the number of subsets!
# n elements → 2^n subsets → O(2^n) timeInteractive O(2^n) Fibonacci Demo
Naive Fibonacci - O(2^n) Recursive Explosion
Interactive Demo: Subset Generation Explosion! 💥
Subset Generation - O(2^n) Combinatorial Explosion 🎯
Interactive Demo: Password Strength Analyzer! 🔐
Exponential Security Growth! 🛡️
Password Strength Analysis in Python 💻
# How many possible passwords?
def count_passwords(length, alphabet_size):
return alphabet_size ** length
# Test different password complexities
lengths = [4, 6, 8, 10, 12]
for length in lengths:
# lowercase letters only (26 characters)
simple = count_passwords(length, 26)
# letters + digits + symbols (94 characters)
complex_pwd = count_passwords(length, 94)
print(f"{length} chars: {simple:,} vs {complex_pwd:,}")Investigation Questions 🤔
- 🔢 4-digit PIN vs 8-character password: How much stronger is longer?
- ⚡ Symbol Power: Why do security experts love special characters?
- 📈 Exponential Growth: Can you spot the pattern as length increases?
- 🎯 Real-World Impact: How do hackers exploit weak passwords?
Interactive Demo: Binary Tree Path Counter! 🌳
Binary Decision Tree - O(2^n) Path Explosion
Python O(2^n) Examples - The Slow Ones!
Recursive Algorithms 🔄
import time
# Naive Fibonacci - O(2^n)
def fib_exponential(n):
if n <= 1:
return n
return fib_exponential(n-1) + fib_exponential(n-2)
# Optimized Fibonacci - O(n)
def fib_linear(n):
if n <= 1:
return n
a, b = 0, 1
for _ in range(2, n + 1):
a, b = b, a + b
return b
# Performance comparison
def compare_fibonacci(n):
# Time the exponential version
start = time.time()
result_exp = fib_exponential(n)
exp_time = time.time() - start
# Time the linear version
start = time.time()
result_lin = fib_linear(n)
lin_time = time.time() - start
print(f"Fibonacci({n}) = {result_exp}")
print(f"Exponential O(2^n): {exp_time:.6f} seconds")
print(f"Linear O(n): {lin_time:.6f} seconds")
print(f"Speedup: {exp_time/lin_time:.0f}x faster!")
# Try compare_fibonacci(30) - dramatic difference!Combinatorial Problems 🎲
# Generate all possible combinations - O(2^n)
def power_set(items):
"""
Generate all possible subsets (power set) of the given items.
Uses recursive approach where each element can either be included or excluded.
Time complexity: O(2^n) where n is the number of items.
"""
# Base case: empty list has only one subset - the empty subset
if not items:
return [[]]
# Take the first item and recursively find power set of remaining items
first = items[0]
rest_subsets = power_set(items[1:]) # Recursive call on remaining items
# For each subset of remaining items, create two versions:
# 1. Without the first item (already in rest_subsets)
# 2. With the first item added to each subset
with_first = [subset + [first] for subset in rest_subsets]
# Combine both versions: subsets without first + subsets with first
return rest_subsets + with_first
# Traveling Salesman Problem (brute force) - O(n!)
def tsp_brute_force(cities, current_city=0, visited=None, path=None):
"""
Solve Traveling Salesman Problem using brute force approach.
Tries all possible routes and returns the shortest one.
Time complexity: O(n!) - factorial time, very slow for large inputs.
Args:
cities: Distance matrix or list of cities
current_city: Current position (default: start at city 0)
visited: Set of already visited cities
path: Current path taken so far
Returns:
Tuple of (best_path, best_distance)
"""
# Initialize on first call: start at city 0 with empty visited set and path
if visited is None:
visited = {current_city} # Set to track visited cities
path = [current_city] # List to track the route taken
# Base case: if we've visited all cities, return to start (city 0)
if len(visited) == len(cities):
complete_path = path + [0] # Add return trip to starting city
total_distance = calculate_distance(complete_path)
return complete_path, total_distance
# Initialize variables to track the best solution found so far
best_path = None
best_distance = float('inf') # Start with infinite distance
# Try visiting each unvisited city next
for next_city in range(len(cities)):
if next_city not in visited: # Only consider unvisited cities
# Recursively solve for the remaining cities
new_path, distance = tsp_brute_force(
cities,
next_city, # Move to this city next
visited | {next_city}, # Add this city to visited set
path + [next_city] # Add this city to current path
)
# Keep track of the best (shortest) route found so far
if distance < best_distance:
best_distance = distance
best_path = new_path
return best_path, best_distance
# Warning: TSP is O(n!) which is even worse than O(2^n)!
# For n cities, we have (n-1)! possible routes to check
def calculate_distance(path):
"""
Calculate the total distance for a given path through cities.
This is a simplified version using a predefined distance matrix.
In a real application, you would calculate distances using coordinates.
Args:
path: List of city indices representing the route
Returns:
Total distance of the path
"""
# Predefined distance matrix for a 3-city example
# In practice, this would be calculated from city coordinates
# using formulas like Euclidean distance: sqrt((x2-x1)² + (y2-y1)²)
distances = {
(0, 1): 10, (1, 0): 10, # Distance between city 0 and city 1
(0, 2): 15, (2, 0): 15, # Distance between city 0 and city 2
(1, 2): 20, (2, 1): 20, # Distance between city 1 and city 2
(0, 0): 0, (1, 1): 0, (2, 2): 0 # Distance from city to itself is 0
}
total = 0 # Initialize total distance
# Sum up distances between consecutive cities in the path
for i in range(len(path) - 1):
current_city = path[i]
next_city = path[i + 1]
# Get distance between current and next city, default to high cost if not found
total += distances.get((current_city, next_city), 100)
return total
# Example usage and testing
if __name__ == "__main__":
"""
Main execution block - runs only when script is executed directly.
Demonstrates both the power set generation and TSP solving algorithms.
"""
# Test the power set generation algorithm
print("Power Set Example:")
print("=" * 40)
items = [1, 2, 3] # Test with a simple 3-element set
result = power_set(items)
print(f"Power set of {items}: {result}")
print(f"Number of subsets: {len(result)} (should be 2^{len(items)} = {2**len(items)})")
print("This demonstrates exponential growth: each new item doubles the subsets!")
print("\nTraveling Salesman Problem Example:")
print("=" * 40)
# Simple 3-city example with predefined distances
# Note: cities parameter is not actually used in our simplified version
# The distance calculation uses the hardcoded distance matrix instead
cities = [[0, 10, 15], [10, 0, 20], [15, 20, 0]] # Distance matrix (not used in current implementation)
print("Solving TSP for 3 cities using brute force...")
print("This will check all possible routes and find the shortest one.")
# Find the optimal path
path, distance = tsp_brute_force(cities)
print(f"Best path found: {path}")
print(f"Total distance: {distance}")
print(f"For {len(cities)} cities, we checked {len(cities)-1}! = {1 if len(cities)<=1 else eval('*'.join(map(str, range(1, len(cities)))))} possible routes.")The Exponential Wall of Pain 💔🤕
Performance Warning ⚠️ fibonacci_slow(40) = ~2 billion function calls! That’s why we need better algorithms for recursive problems.🎯
When O(2^n) Becomes Unusable 🧱
Exponential algorithms hit a “wall” where they become practically impossible to run.
The Exponential Timeline ⏰
| Input Size | Operations | Time* | Real-World Impact |
|---|---|---|---|
| 10 | 1,024 | 0.001s | Barely noticeable |
| 20 | 1,048,576 | 1s | Starting to wait |
| 25 | 33,554,432 | 30s | Getting annoying |
| 30 | 1,073,741,824 | 15 minutes | Time for coffee |
| 35 | 34,359,738,368 | 8 hours | Overnight job |
| 40 | 1,099,511,627,776 | 12 days | Vacation time |
| 50 | 1,125,899,906,842,624 | 35 years | Career change |
| 60 | ~10^18 | 1,000 years | Wait for next millennium |
*Approximate times for simple operations
Real Performance Testing 🧪
import time
def fibonacci_naive(n):
if n <= 1:
return n
return fibonacci_naive(n-1) + fibonacci_naive(n-2)
# Test with increasing values
test_values = [10, 15, 20, 25, 30]
print("n\tTime (seconds)\tGrowth Factor")
print("-" * 40)
previous_time = None
for n in test_values:
start = time.time()
result = fibonacci_naive(n)
duration = time.time() - start
growth_factor = ""
if previous_time:
factor = duration / previous_time
growth_factor = f"{factor:.1f}x"
print(f"{n}\t{duration:.3f}\t\t{growth_factor}")
previous_time = duration
# Stop if taking too long
if duration > 10: # More than 10 seconds
print(f"Stopping at n={n} - taking too long!")
breakBy The Way, … 🧪
Q: Is there a shorter way to produce the Fibonacci sequence?
A: Absolutely! Use Binet’s formula.
import math
def fibonacci_binet(n):
"""
Calculates the nth Fibonacci number using Binet's formula.
Args:
n: The index of the Fibonacci number to calculate (non-negative integer).
Returns:
The nth Fibonacci number as an integer.
"""
if n < 0:
raise ValueError("Input 'n' must be a non-negative integer.")
if n == 0:
return 0
if n == 1:
return 1
phi = (1 + math.sqrt(5)) / 2
psi = (1 - math.sqrt(5)) / 2
# Binet's formula
fn = (phi**n - psi**n) / math.sqrt(5)
# Round to the nearest integer as Binet's formula can produce
# slight floating-point inaccuracies for large n.
return int(round(fn))
### Execute the code here
for i in range(11):
print(f"Fibonacci({i}) = {fibonacci_binet(i)}")
# Test with a larger number
n_large = 20
print(f"\n Larger:\nFibonacci({n_large}) = {fibonacci_binet(n_large)}")Important
Q: What is the complexity of this algorithm?
Partner Investigation: The Exponential Explosion!
Run these samples of code with a partner. Discuss outcomes and respond to questions at the end of the source code.
Partner Activity 👥
⚠️ WARNING: These experiments can take a VERY long time! Partner coordination is essential.
Experiment 1: Fibonacci Explosion Investigation
"""
EXPONENTIAL COMPLEXITY ANALYSIS - Fibonacci Performance Tracking
================================================================
Educational Purpose:
This program provides hands-on experience with exponential time complexity O(2^n)
through a carefully instrumented naive Fibonacci implementation. Students observe
how function calls grow exponentially, creating an intuitive understanding of why
certain algorithms become computationally intractable as input size increases.
Key Learning Objectives:
1. Experience exponential growth patterns firsthand through performance tracking
2. Understand the relationship between algorithm structure and time complexity
3. Develop intuition for computational limits and practical algorithm constraints
4. Learn safe experimentation practices with potentially expensive algorithms
5. Motivate the need for algorithmic optimization techniques
What This Program Demonstrates:
- Naive Recursive Fibonacci: O(2^n) time complexity with detailed call tracking
- Performance metrics: function call counts, recursion depth, execution time
- Safety protocols: controlled testing environment with automatic limits
- Educational scaffolding: partner-based learning with guided analysis questions
Target Audience: CS 101 students learning about algorithm complexity analysis
Companion to: complex_2.py (optimization comparison) and interactive presentations
Author: Course Materials for Algorithm Analysis Unit
Date: Fall 2025
"""
# Import required modules for timing and system recursion limits
import time
import sys
def fib_naive_with_tracking(n, depth=0, memo=None):
"""
Naive recursive Fibonacci implementation with performance tracking.
This function demonstrates O(2^n) exponential time complexity by:
- Making two recursive calls for each non-base case
- Tracking the total number of function calls made
- Tracking the maximum recursion depth reached
Args:
n (int): The Fibonacci number to calculate
depth (int): Current recursion depth (for tracking purposes)
memo (dict): Dictionary to track performance metrics
Returns:
tuple: (fibonacci_result, performance_stats)
"""
# Initialize tracking dictionary on first call
if memo is None:
memo = {'calls': 0, 'max_depth': 0}
# Count this function call and update maximum depth reached
memo['calls'] += 1
memo['max_depth'] = max(memo['max_depth'], depth)
# Base case: F(0) = 0, F(1) = 1
if n <= 1:
return n, memo
# Recursive case: F(n) = F(n-1) + F(n-2)
# This creates the exponential explosion - each call makes TWO more calls
left_result, memo = fib_naive_with_tracking(n-1, depth+1, memo)
right_result, memo = fib_naive_with_tracking(n-2, depth+1, memo)
# Return the sum of the two recursive results plus performance data
return left_result + right_result, memo
# SAFETY PROTOCOL - Partner coordination essential!
# Partner A: Test [5, 10, 15]
# Partner B: Test [20, 25] ONLY (DO NOT go higher without permission!)
def safe_fibonacci_test(test_values, max_time=30):
"""
Safely test Fibonacci calculations with performance monitoring.
This function provides a controlled environment for testing the exponential
Fibonacci algorithm by:
- Setting time limits to prevent infinite waiting
- Adjusting recursion limits to prevent stack overflow
- Collecting and displaying performance metrics
- Stopping execution if calculations take too long
Args:
test_values (list): List of Fibonacci numbers to calculate
max_time (int): Maximum seconds allowed per calculation
Returns:
list: Results containing performance data for each test
"""
results = [] # Store performance results for analysis
# Test each Fibonacci number in the provided list
for n in test_values:
print(f"\nTesting Fibonacci({n})...")
# Record start time to measure execution duration
start = time.time()
try:
# Prevent stack overflow by increasing recursion limit
# Exponential algorithms can create very deep recursion
old_limit = sys.getrecursionlimit()
sys.setrecursionlimit(max(1000, n * 100)) # Scale with input size
# Execute the Fibonacci calculation with tracking
result, stats = fib_naive_with_tracking(n)
duration = time.time() - start
# Restore original recursion limit
sys.setrecursionlimit(old_limit)
# Safety check: Stop if calculation takes too long
# This prevents students from waiting indefinitely for large inputs
if duration > max_time:
print(f"⚠️ STOPPED: Taking too long ({duration:.2f}s)")
break
# Store performance data for analysis
results.append({
'n': n, # Input value
'result': result, # Fibonacci result
'calls': stats['calls'], # Total function calls (shows 2^n growth)
'max_depth': stats['max_depth'], # Maximum recursion depth
'time': duration # Execution time in seconds
})
# Display results to show exponential growth pattern
print(f"Result: {result}")
print(f"Function calls: {stats['calls']:,}") # Comma-separated for readability
print(f"Time: {duration:.4f} seconds")
except RecursionError:
# Handle case where recursion goes too deep
print(f"⚠️ RECURSION LIMIT EXCEEDED for n={n}")
break
return results
# ===================================================================
# MAIN EXECUTION SECTION - Educational Assignment for Partner Learning
# ===================================================================
"""
This section provides a structured learning experience about exponential complexity.
Students work in pairs with different test values to observe O(2^n) growth patterns.
The assignment is designed to be:
1. Safe - preventing system crashes with controlled inputs
2. Educational - showing clear exponential growth patterns
3. Collaborative - partners compare results to understand scaling
"""
# YOUR ASSIGNMENT (choose based on partner role):
# These values are carefully chosen to demonstrate exponential growth
# while keeping execution times reasonable for classroom use
my_test_values = [5, 10, 15] # Partner A - safe values that complete quickly
# my_test_values = [20, 25] # Partner B - be VERY careful! These take much longer
# Execute the performance test with your chosen values
# This will show you exactly how O(2^n) algorithms behave in practice
results = safe_fibonacci_test(my_test_values)
# ===================================================================
# ANALYSIS FRAMEWORK - Questions to Guide Student Understanding
# ===================================================================
# After running your tests, discuss these questions with your partner:
# 1. How did function calls grow with each increase in n?
# (Look for the pattern: roughly doubling with each increment)
# 2. Can you predict the pattern?
# (Try to predict calls for n+1 based on your observed data)
# 3. Why does this get so slow so quickly?
# (Connect the exponential call growth to exponential time complexity)
# 4. What would happen with larger inputs?
# (Extrapolate from your data - why do we need iterative approaches?)
"""
Expected Learning Outcomes:
- Visceral understanding of exponential growth rates
- Appreciation for algorithm efficiency importance
- Motivation to learn optimized algorithms (dynamic programming, memoization)
- Understanding of why certain problems become computationally intractable
"""Experiment 2: Optimization Race Challenge
"""
ALGORITHM OPTIMIZATION DEMONSTRATION - Fibonacci Performance Comparison
========================================================================
Educational Purpose:
This program demonstrates the dramatic performance differences between three
approaches to computing Fibonacci numbers, showing students why algorithm
optimization matters in real-world programming.
Key Learning Objectives:
1. Experience the practical impact of Big O complexity
2. Understand how memoization transforms exponential to linear time
3. Compare recursive vs iterative solutions
4. Witness exponential algorithms becoming computationally intractable
Three Approaches Compared:
- Naive Recursive: O(2^n) - exponential time, exponential space
- Memoized Recursive: O(n) - linear time, linear space
- Iterative: O(n) - linear time, constant space
Target Audience: CS 101 students learning about algorithm complexity
Author: Course Materials for Algorithm Analysis Unit
Date: Fall 2025
"""
from functools import lru_cache # Python's built-in memoization decorator
import time # For precise performance timing
# ===================================================================
# THREE FIBONACCI IMPLEMENTATIONS - Different Complexity Classes
# ===================================================================
def fib_exponential(n):
"""
NAIVE RECURSIVE FIBONACCI - O(2^n) Time Complexity
This is the "textbook" recursive implementation that directly follows
the mathematical definition: F(n) = F(n-1) + F(n-2)
Why It's Exponential:
- Each call spawns two more calls (binary tree of recursion)
- Massive redundant calculation (F(5) calculated multiple times)
- Total calls ≈ 2^n, making it impractical for n > 35
Educational Value: Shows students why naive approaches can be disastrous
Args:
n (int): The position in Fibonacci sequence to calculate
Returns:
int: The nth Fibonacci number
Time Complexity: O(2^n) - exponential growth
Space Complexity: O(n) - recursion stack depth
"""
# Base cases: F(0) = 0, F(1) = 1
if n <= 1:
return n
# Recursive case: F(n) = F(n-1) + F(n-2)
# WARNING: This creates exponential redundancy!
return fib_exponential(n-1) + fib_exponential(n-2)
@lru_cache(maxsize=None) # Python decorator for automatic memoization
def fib_memoized(n):
"""
MEMOIZED RECURSIVE FIBONACCI - O(n) Time Complexity
Same recursive structure as naive version, but with caching!
The @lru_cache decorator automatically stores results, eliminating
redundant calculations that made the naive version exponential.
How Memoization Works:
- First call to F(k): calculated and stored in cache
- Subsequent calls to F(k): returned instantly from cache
- Transforms exponential tree into linear sequence
Educational Value: Shows power of caching/dynamic programming
Args:
n (int): The position in Fibonacci sequence to calculate
Returns:
int: The nth Fibonacci number
Time Complexity: O(n) - each F(k) calculated only once
Space Complexity: O(n) - cache storage + recursion stack
"""
# Base cases: F(0) = 0, F(1) = 1
if n <= 1:
return n
# Recursive case with automatic memoization
# The @lru_cache decorator handles caching transparently
return fib_memoized(n-1) + fib_memoized(n-2)
def fib_iterative(n):
"""
ITERATIVE FIBONACCI - O(n) Time, O(1) Space
Bottom-up approach that builds the sequence from F(0) to F(n).
No recursion needed - just a simple loop with two variables.
Why It's Optimal:
- Linear time: exactly n-1 iterations for F(n)
- Constant space: only stores current and previous values
- No function call overhead or stack risk
- Most practical approach for large n
Educational Value: Shows how iterative thinking can optimize recursive problems
Args:
n (int): The position in Fibonacci sequence to calculate
Returns:
int: The nth Fibonacci number
Time Complexity: O(n) - single loop from 2 to n
Space Complexity: O(1) - only two variables needed
"""
# Handle base cases directly
if n <= 1:
return n
# Initialize: a = F(0), b = F(1)
a, b = 0, 1
# Build sequence iteratively: F(2), F(3), ..., F(n)
for _ in range(2, n + 1):
# Calculate next Fibonacci number and shift variables
# This elegant swap calculates F(i) = F(i-1) + F(i-2)
a, b = b, a + b
return b # b now contains F(n)
def optimization_race(n_values):
"""
PERFORMANCE COMPARISON ENGINE - Algorithm Racing Framework
This function conducts a systematic performance comparison of all three
Fibonacci implementations, providing students with concrete evidence of
how algorithm choice affects real-world performance.
Educational Design Features:
- Automatic safety checks (skips exponential for large n)
- Precise timing measurements using time.time()
- Clear performance reporting with speedup calculations
- Fair testing (cache clearing between runs)
- Robust exception handling for edge cases
Args:
n_values (list): Fibonacci numbers to test (e.g., [10, 20, 30])
Returns:
None (prints results directly for classroom demonstration)
Raises:
ValueError: If n_values contains invalid inputs
TypeError: If n_values is not iterable
"""
# Input validation to prevent errors
try:
# Check if n_values is iterable
iter(n_values)
except TypeError:
raise TypeError("n_values must be an iterable (list, tuple, etc.)")
# Validate each value in the input
valid_values = []
for n in n_values:
try:
n = int(n) # Convert to integer if possible
if n < 0:
print(f"⚠️ WARNING: Skipping negative value {n} (Fibonacci undefined for negative numbers)")
continue
if n > 1000:
print(f"⚠️ WARNING: Skipping extremely large value {n} (potential memory/time issues)")
continue
valid_values.append(n)
except (ValueError, TypeError):
print(f"⚠️ WARNING: Skipping invalid value {n} (must be a non-negative integer)")
continue
if not valid_values:
print("❌ ERROR: No valid values to test!")
return
print("🏁 Fibonacci Optimization Race!")
print("=" * 50)
print("Testing three approaches: Exponential vs Memoized vs Iterative")
print(f"Valid test values: {valid_values}")
for n in valid_values:
print(f"\n🧮 Computing Fibonacci({n}):")
# ===== EXPONENTIAL APPROACH - O(2^n) =====
# Safety check: only test exponential for manageable values
# Beyond n=35, exponential becomes impractically slow
if n <= 30:
try:
start = time.time() # Start timing
result_exp = fib_exponential(n)
exp_time = time.time() - start # Calculate duration
print(f" 📈 Exponential O(2^n): {exp_time:.6f}s")
except RecursionError:
print(f" 📈 Exponential O(2^n): FAILED (recursion limit exceeded)")
exp_time = float('inf')
result_exp = None
except OverflowError:
print(f" 📈 Exponential O(2^n): FAILED (number too large)")
exp_time = float('inf')
result_exp = None
except Exception as e:
print(f" 📈 Exponential O(2^n): ERROR ({type(e).__name__})")
exp_time = float('inf')
result_exp = None
else:
print(f" 📈 Exponential O(2^n): SKIPPED (too slow!)")
exp_time = float('inf') # Mark as infinite time for comparisons
result_exp = None
# ===== MEMOIZED APPROACH - O(n) =====
# Clear any previous cache to ensure fair timing comparison
try:
fib_memoized.cache_clear() # Reset memoization cache
start = time.time()
result_memo = fib_memoized(n)
memo_time = time.time() - start
print(f" 🧠 Memoized O(n): {memo_time:.6f}s")
except RecursionError:
print(f" 🧠 Memoized O(n): FAILED (recursion limit exceeded)")
memo_time = float('inf')
result_memo = None
except OverflowError:
print(f" 🧠 Memoized O(n): FAILED (number too large)")
memo_time = float('inf')
result_memo = None
except Exception as e:
print(f" 🧠 Memoized O(n): ERROR ({type(e).__name__})")
memo_time = float('inf')
result_memo = None
# ===== ITERATIVE APPROACH - O(n) =====
try:
start = time.time()
result_iter = fib_iterative(n)
iter_time = time.time() - start
print(f" 🔄 Iterative O(n): {iter_time:.6f}s")
except OverflowError:
print(f" 🔄 Iterative O(n): FAILED (number too large)")
iter_time = float('inf')
result_iter = None
except Exception as e:
print(f" 🔄 Iterative O(n): ERROR ({type(e).__name__})")
iter_time = float('inf')
result_iter = None
# ===== PERFORMANCE ANALYSIS =====
# Calculate and display speedup ratios if exponential was testable
# This shows students the dramatic impact of optimization
if exp_time != float('inf'):
try:
# Calculate speedup ratios with division by zero protection
if memo_time > 0:
memo_speedup = exp_time / memo_time
print(f" 🚀 Memoized speedup: {memo_speedup:.0f}x faster!")
else:
print(f" 🚀 Memoized speedup: EXTREMELY FAST (sub-microsecond)")
if iter_time > 0:
iter_speedup = exp_time / iter_time
print(f" 🚀 Iterative speedup: {iter_speedup:.0f}x faster!")
else:
print(f" 🚀 Iterative speedup: EXTREMELY FAST (sub-microsecond)")
except ZeroDivisionError:
# Fallback protection in case of unexpected zero division
print(f" 🚀 Speedup calculation: EXTREMELY FAST (division by zero avoided)")
print(f" 📊 Optimized versions completed in negligible time!")
# Verify all methods produce the same result (when all succeeded)
try:
# Only verify if all results are available and not None
if all(result is not None for result in [result_exp, result_memo, result_iter]):
assert result_exp == result_memo == result_iter, "Results don't match!"
print(f" ✅ All methods produced identical results: {result_iter}")
else:
# Some calculations failed, show what we have
available_results = []
if result_memo is not None:
available_results.append(f"Memoized: {result_memo}")
if result_iter is not None:
available_results.append(f"Iterative: {result_iter}")
if result_exp is not None:
available_results.append(f"Exponential: {result_exp}")
if available_results:
print(f" 📊 Available results: {', '.join(available_results)}")
# Verify the ones we have match
valid_results = [r for r in [result_exp, result_memo, result_iter] if r is not None]
if len(valid_results) > 1 and len(set(valid_results)) == 1:
print(f" ✅ Available results match!")
elif len(valid_results) > 1:
print(f" ❌ WARNING: Available results don't match!")
except AssertionError as e:
print(f" ❌ ERROR: {e}")
print(f" Exponential: {result_exp if result_exp is not None else 'FAILED'}")
print(f" Memoized: {result_memo if result_memo is not None else 'FAILED'}")
print(f" Iterative: {result_iter if result_iter is not None else 'FAILED'}")
else:
# For large n, exponential is too slow to test
print(f" ⚡ Exponential would take HOURS/DAYS for n={n}")
print(f" ⚡ Optimization makes impossible problems solvable!")
# ===================================================================
# MAIN EXECUTION - Structured Partner Learning Experience
# ===================================================================
"""
COLLABORATIVE ASSIGNMENT STRUCTURE:
Students work in pairs with different test cases to observe how algorithm
choice affects performance across different problem sizes.
Partner A: Tests smaller values where all approaches are feasible
Partner B: Tests larger values where exponential becomes impossible
This design helps students experience the "complexity cliff" - the point
where poor algorithms become computationally intractable.
"""
# CHOOSE YOUR PARTNER ROLE:
# Uncomment the appropriate line based on your assignment
my_values = [10, 20, 30] # Partner A: All approaches testable
# my_values = [35, 40, 50] # Partner B: Exponential becomes impossible!
print("🎯 RUNNING OPTIMIZATION COMPARISON...")
print("Your test values:", my_values)
print()
# Execute the performance comparison
optimization_race(my_values)
# ===================================================================
# ANALYSIS FRAMEWORK - Post-Experiment Discussion Questions
# ===================================================================
print("\n" + "="*60)
print("📚 DISCUSSION QUESTIONS FOR PARTNERS:")
print("="*60)
print()
print("After reviewing your results, discuss these questions:")
print()
print("1. 🤔 TIPPING POINT: At what value of n does exponential become unusable?")
print(" (Partner A vs B will have different experiences)")
print()
print("2. 🚀 SPEEDUP MAGNITUDE: How dramatic is the speedup from optimization?")
print(" (Look at the 'X times faster' numbers)")
print()
print("3. 🧠 MEMOIZATION MAGIC: Why does memoization work so well here?")
print(" (Think about redundant calculations in the exponential version)")
print()
print("4. 💡 REAL-WORLD IMPACT: What does this teach us about algorithm choice?")
print(" (Consider: debugging vs production, small vs large datasets)")
print()
print("5. 🔄 SPACE VS TIME: Compare memoized vs iterative - which is better?")
print(" (Consider memory usage and practical constraints)")
"""
Expected Learning Outcomes:
- Visceral understanding of exponential vs linear complexity
- Appreciation for the power of dynamic programming/memoization
- Recognition that algorithm choice can make impossible problems solvable
- Understanding of trade-offs between different optimization approaches
- Motivation to learn more advanced algorithmic techniques
"""Final Challenge: Algorithm Detective! 🕵️♂️
Can You Identify These Complexities Part 1? 🧩
Mystery Algorithms: Put Your Skills to the Test! 🤔 * Test your new Big-O analysis skills with these code snippets! * Look for loops, recursion, and data access patterns!
Final Challenge: Continued! 🕵️♂️
Can You Identify These Complexities Part II? 🧩
The Answers: How Did You Do? ✅
🎉 Algorithm Analysis Revealed!
Check your detective work against these solutions:
✅🎉 ✅🎉 ✅🎉 ✅🎉