Chapter 4: SOME SIMPLE NUMERICAL PROGRAMS

Some Approximation Techniques in Python: Numerical Search Methods and Their Applications

CS 101 - Fall 2025

Course Overview

So, What are we talking about today?

• To understand exhaustive enumeration and iterative numerical techniques for approximation
• To study and understand how algorithms use approximations to find square and cube roots
• Compare efficiency of different approximation methods, and some of their limitations
• To explore primality testing using enumeration
• Implement practical Python solutions (code)

Part1: Exhaustive Method

Simple Exhaustive Square Roots

# Exhaustive square root
def simple_square_root(x):
    # find a root of a perfect root
    ans = 0
    while ans **2 < abs(x):
        ans += 1
    if ans**2 != abs(x):
        print(f"x = {x} is not perfect square root...")
    else:
        if x<0:
            ans =-ans
        print(f"Square root of {x} is {ans}.")

We count and then square the result to compare to the absolute value of the number to check.

Testing the Prototype

simple_square_root(25) # find the square root of a square.

Square root of 25 is 5.

 

simple_square_root(26) # not a square ...

x = 26 is not perfect square root...

simple_square_root(x)

Count, square and check

Step-by-Step Process:

1. Start with ans = 0
2. Check if ans² < |x|
3. If true, increment ans by 1
4. Repeat until ans² ≥ |x|
5. Test if ans² exactly equals |x|

Key Logic: Exhaustive search: Tests every integer sequentially.

If ans² == |x| then the root is found. Cool!

Binary outcome: Either finds exact root or reports failure

Example: For x = 25,

tests: 0^2, 1^2, 2^2, 3^2, 4^2, 5^2 = 25 ✓

Be careful!

Example: For x = 26,

tests: 0^2, 1^2, 2^2, 3^2, 4^2, 5^2, 6^2 != 26

(We just passed the correct value!!)

Simple Exhaustive Cube Roots (with same method)

 

# Exhaustive cube root
def simple_cube_root(x):
    # find a root of a perfect root
    ans = 0
    while ans **3 < abs(x):
        ans += 1
    if ans**3 != abs(x):
        print(f"x = {x} is not perfect cube root...")
    else:
        if x<0:
            ans =-ans
        print(f"Cube root of {x} is {ans}.")

Testing the Prototype

simple_cube_root(8) # has a cube root

Cube root of 8 is 2.

 

simple_cube_root(7) # does not have a cube ...

x = 7 is not perfect cube root...

 

simple_cube_root(x)

Count, cube and check

Step-by-Step Process:

(Same as before)

1. Start with ans = 0
2. Check if ans^3 < |x|
3. If true, increment ans by 1
4. Repeat until ans^3 ≥ |x|
5. Test if ans^3 exactly equals |x|

Key Logic: Exhaustive search: Tests every integer sequentially.

If ans^3 == |x| then the root is found. Nifty!

Binary outcome: Either finds exact root or reports failure

 

Example: For x = 8,

tests: 0^3, 1^3, 2^3 = 8 ✓

Be careful!

For x = 9, tests: 0^3, 1^3, 2^3, 3^3 != 9

(We just passed the correct value!!)

How to Generalize This?

Exhaustive nth root

def simple_n_root(x, n):
    # find a root of a perfect root
    ans = 0
    while ans **n < abs(x):
        ans += 1
    if ans**n != abs(x):
        print(f"x = {x} is not perfect {n} root...")
    else:
        if x<0:
            ans =-ans
        print(f"{n} root of {x} is {ans}.")

Testing the Prototype

simple_n_root(8,2) # find the square root

x = 8 is not perfect 2 root...

 

simple_n_root(17,2) # not a square ...

x = 17 is not perfect 2 root...

 

simple_n_root(9,3) # not a cube ...

x = 9 is not perfect 3 root...

 

Complicated Exhaustive Square Roots

Add print statements to see steps.

def exhaustive_sqrt(x, epsilon=0.01):
    """
    Find square root using exhaustive enumeration
    """
    step = epsilon
    num_guesses = 0
    ans = 0.0
    
    print(f"Finding square root of {x}")
    
    while abs(ans**2 - x) >= epsilon and ans*ans <= x:
        ans += step
        num_guesses += 1
    
    print(f"Number of guesses: {num_guesses}")
    
    if abs(ans**2 - x) >= epsilon:
        print(f"Failed to find square root of {x}")
        return None
    else:
        print(f"Square root of {x} is approximately {ans}")
        return ans

Testing the Prototype

exhaustive_sqrt(25) # find the square root of a square.

Finding square root of 25
Number of guesses: 500
Square root of 25 is approximately 4.999999999999938

4.999999999999938

exhaustive_sqrt(26) # Not a square ...

Finding square root of 26
Number of guesses: 510
Square root of 26 is approximately 5.099999999999936

5.099999999999936

How This Code Works:

Algorithm Steps: 1. Start with ans = 0.0 2. Increment by epsilon each iteration 3. Check if ans² is close enough to x 4. Stop when within tolerance or exceeded target

Key Variables: - step: How much to increment each guess - num_guesses: Performance counter - ans: Current approximation

Loop Condition Explained: - abs(ans**2 - x) >= epsilon: Not accurate enough yet - ans*ans <= x: Haven’t exceeded target (prevents infinite loop)

Why It Works: - Systematically tests every possible value - Guaranteed to find solution if it exists - Simple but inefficient for large numbers

The Fundamental Limitation

These functions use “exhaustive enumeration” over integers:

• Perfect squares/cubes: Have integer roots (4, 9, 16, 25…)
• Non-perfect squares/cubes: Have irrational/decimal roots

Key Insight: The algorithm design assumes the answer is an integer!

# This works:
simple_square_root (25) = 5
simple_square_root(27) = 3

# (only exact integers)

# This fails:
simple_square_root(26) = 5.099... 
simple_cube_root(26) = 2.962...

# (not integers, no results found

Part2: Approximation

What if I need exact numbers for roots of a non-perfect value?

My number is …

• Not a square
• Not a cube
• Not an \(n^{th}\) value of anything!

How to find exact values of any number I want?!

What We Need Instead

For approximating non-perfect roots, we need:

1. Decimal precision (not just integers)
2. Tolerance/epsilon (how close is “close enough?”)
3. Different search strategies:
   • Increment by small decimals (0.01, 0.001…)
   • Newton’s method

Next: We’ll explore these approximation techniques!

So, What is Approximation?

Key Concepts:

• Finding “good enough” solutions
• Trading precision for efficiency
• Iterative refinement
• Stopping criteria (stop the approximation by setting precision)

Like, Why Approximation?

• Exact solutions may not exist (not a perfect number)
• Real-world applications (like how your computer does this root-finding!)

Issac Newton

Whoops, here’s the right slide.

(Issac Newton)

Square Root Approximation with Newton’s Method

def newtons_sqrt(n:float, guess:float = 1.0) -> float:
    while abs(n - guess*guess) > .0001:
        print(f"n = {n}, guess = {guess}")
        print(f"   abs(n - guess*guess) = {abs(n - guess*guess)}")
        guess = guess - (guess*guess - n)/(2*guess)
        print(f"   guess = guess - (guess*guess - n)/(2*guess) = {guess}\n")

    return guess

Test using debug print statements …

my_num = 25
result = newtons_sqrt(my_num)
print(f"Verification:\n {result}^2 = ")
print(f"{result**2} is {result**2 == result**2}")

n = 25, guess = 1.0
   abs(n - guess*guess) = 24.0
   guess = guess - (guess*guess - n)/(2*guess) = 13.0

n = 25, guess = 13.0
   abs(n - guess*guess) = 144.0
   guess = guess - (guess*guess - n)/(2*guess) = 7.461538461538462

n = 25, guess = 7.461538461538462
   abs(n - guess*guess) = 30.674556213017752
   guess = guess - (guess*guess - n)/(2*guess) = 5.406026962727994

n = 25, guess = 5.406026962727994
   abs(n - guess*guess) = 4.22512752174206
   guess = guess - (guess*guess - n)/(2*guess) = 5.015247601944898

n = 25, guess = 5.015247601944898
   abs(n - guess*guess) = 0.15270850881405096
   guess = guess - (guess*guess - n)/(2*guess) = 5.000023178253949

n = 25, guess = 5.000023178253949
   abs(n - guess*guess) = 0.00023178307672111487
   guess = guess - (guess*guess - n)/(2*guess) = 5.000000000053723

Verification:
 5.000000000053723^2 = 
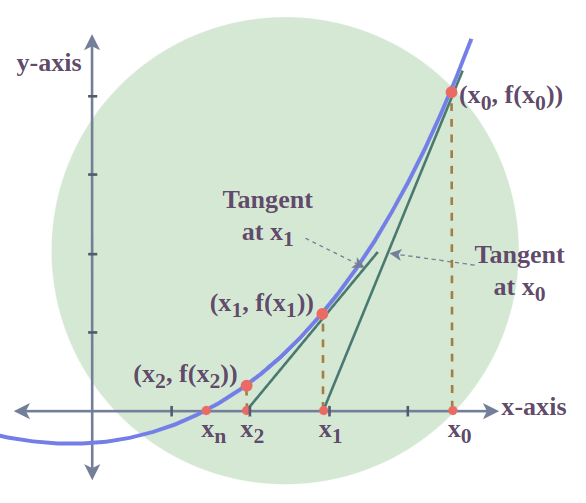
25.00000000053723 is True

So, how does this thing work?

• Each approximation of \(x\) is from Equation: \(x_{n+1} = x_{n} - \frac{f(x_{n})}{f'(x_{n})}\)
  • We approach the actual value with each iteration
• The \(\frac{f(x_{n})}{f'(x_{n})}\) term allows for us to get closer to the actual number with each approximation.
  • \(x_{0}\) to \(x_{1}\) to \(x_{2}\) to, …, to \(x_{n}\)

Cube Roots

def newtons_cube_root(n:float, guess:float = 1.0) -> float:
    while abs(n - guess*guess*guess) > .0001:
        print(f"n = {n}, guess = {guess}")
        print(f"   abs(n - guess^3) = {abs(n - guess*guess*guess)}")
        guess = guess - (guess*guess*guess - n)/(3*(guess*guess))
        print(f"   guess = guess - (guess*guess*guess - n)/(3*(guess*guess)) = {guess}\n")
    return guess

Testing the Prototype

newtons_cube_root(8)

n = 8, guess = 1.0
   abs(n - guess^3) = 7.0
   guess = guess - (guess*guess*guess - n)/(3*(guess*guess)) = 3.3333333333333335

n = 8, guess = 3.3333333333333335
   abs(n - guess^3) = 29.037037037037045
   guess = guess - (guess*guess*guess - n)/(3*(guess*guess)) = 2.462222222222222

n = 8, guess = 2.462222222222222
   abs(n - guess^3) = 6.92731645541838
   guess = guess - (guess*guess*guess - n)/(3*(guess*guess)) = 2.081341247671579

n = 8, guess = 2.081341247671579
   abs(n - guess^3) = 1.0163315496105625
   guess = guess - (guess*guess*guess - n)/(3*(guess*guess)) = 2.003137499141287

n = 8, guess = 2.003137499141287
   abs(n - guess^3) = 0.03770908398584538
   guess = guess - (guess*guess*guess - n)/(3*(guess*guess)) = 2.000004911675504

2.000004911675504

Testing the Prototype

newtons_cube_root(27)

n = 27, guess = 1.0
   abs(n - guess^3) = 26.0
   guess = guess - (guess*guess*guess - n)/(3*(guess*guess)) = 9.666666666666666

n = 27, guess = 9.666666666666666
   abs(n - guess^3) = 876.2962962962961
   guess = guess - (guess*guess*guess - n)/(3*(guess*guess)) = 6.540758356453956

n = 27, guess = 6.540758356453956
   abs(n - guess^3) = 252.82358364070478
   guess = guess - (guess*guess*guess - n)/(3*(guess*guess)) = 4.570876778578707

n = 27, guess = 4.570876778578707
   abs(n - guess^3) = 68.49893783892396
   guess = guess - (guess*guess*guess - n)/(3*(guess*guess)) = 3.4780192333867963

n = 27, guess = 3.4780192333867963
   abs(n - guess^3) = 15.07226932492673
   guess = guess - (guess*guess*guess - n)/(3*(guess*guess)) = 3.0626891086275365

n = 27, guess = 3.0626891086275365
   abs(n - guess^3) = 1.7282216154620045
   guess = guess - (guess*guess*guess - n)/(3*(guess*guess)) = 3.001274406506175

n = 27, guess = 3.001274406506175
   abs(n - guess^3) = 0.03442359474399126
   guess = guess - (guess*guess*guess - n)/(3*(guess*guess)) = 3.0000005410641766

3.0000005410641766

Testing the Prototype

newtons_cube_root(31)

n = 31, guess = 1.0
   abs(n - guess^3) = 30.0
   guess = guess - (guess*guess*guess - n)/(3*(guess*guess)) = 11.0

n = 31, guess = 11.0
   abs(n - guess^3) = 1300.0
   guess = guess - (guess*guess*guess - n)/(3*(guess*guess)) = 7.418732782369146

n = 31, guess = 7.418732782369146
   abs(n - guess^3) = 377.30921842166106
   guess = guess - (guess*guess*guess - n)/(3*(guess*guess)) = 5.133572303084083

n = 31, guess = 5.133572303084083
   abs(n - guess^3) = 104.28792927185404
   guess = guess - (guess*guess*guess - n)/(3*(guess*guess)) = 3.814485354880487

n = 31, guess = 3.814485354880487
   abs(n - guess^3) = 24.501900623588178
   guess = guess - (guess*guess*guess - n)/(3*(guess*guess)) = 3.2531703966218446

n = 31, guess = 3.2531703966218446
   abs(n - guess^3) = 3.4286849761153846
   guess = guess - (guess*guess*guess - n)/(3*(guess*guess)) = 3.1451781175927085

n = 31, guess = 3.1451781175927085
   abs(n - guess^3) = 0.11255922102655447
   guess = guess - (guess*guess*guess - n)/(3*(guess*guess)) = 3.1413852355779674

n = 31, guess = 3.1413852355779674
   abs(n - guess^3) = 0.00013568459873170013
   guess = guess - (guess*guess*guess - n)/(3*(guess*guess)) = 3.14138065239808

3.14138065239808

General Case

def newtons_nth_root(n: int, value: float, guess: float = 1.0) -> float:
    """
    Find the nth root of a value using Newton's method.
    
    Parameters:
    n (int): The root to find (e.g., 2 for square root, 3 for cube root)
    value (float): The value for which to find the nth root
    guess (float): Initial guess (default: 1.0)
    
    Returns:
    float: The nth root of the value
    
    Mathematical formula:
    For finding y such that y^n = value, we use Newton's method:
    y_new = y - f(y)/f'(y)
    where f(y) = y^n - value and f'(y) = n * y^(n-1)
    So: y_new = y - (y^n - value)/(n * y^(n-1))
    """
    if n <= 0:
        raise ValueError("n must be a positive integer")
    if value < 0 and n % 2 == 0:
        raise ValueError("Cannot find even root of negative number")
    
    tolerance = 0.0001
    
    while abs(guess**n - value) > tolerance:
        print(f"n = {n}, value = {value}, guess = {guess}")
        print(f"   abs(guess^n - value) = abs({guess}^{n} - {value}) = {abs(guess**n - value)}")
        
        # Newton's method formula: guess_new = guess - (guess^n - value)/(n * guess^(n-1))
        guess_new = guess - (guess**n - value) / (n * guess**(n-1))
        
        print(f"   guess_new = guess - (guess^n - value)/(n * guess^(n-1))")
        print(f"   guess_new = {guess} - ({guess}^{n} - {value})/({n} * {guess}^{n-1}) = {guess_new}\n")
        
        guess = guess_new
    
    return guess

Testing the Prototype (1)

print("Square root of 16 (n=2, value=16):")
result = newtons_nth_root(2, 16)
print(f"Result: {result}")
print(f"Verification: {result}^2 = {result**2}\n")

Square root of 16 (n=2, value=16):
n = 2, value = 16, guess = 1.0
   abs(guess^n - value) = abs(1.0^2 - 16) = 15.0
   guess_new = guess - (guess^n - value)/(n * guess^(n-1))
   guess_new = 1.0 - (1.0^2 - 16)/(2 * 1.0^1) = 8.5

n = 2, value = 16, guess = 8.5
   abs(guess^n - value) = abs(8.5^2 - 16) = 56.25
   guess_new = guess - (guess^n - value)/(n * guess^(n-1))
   guess_new = 8.5 - (8.5^2 - 16)/(2 * 8.5^1) = 5.1911764705882355

n = 2, value = 16, guess = 5.1911764705882355
   abs(guess^n - value) = abs(5.1911764705882355^2 - 16) = 10.94831314878893
   guess_new = guess - (guess^n - value)/(n * guess^(n-1))
   guess_new = 5.1911764705882355 - (5.1911764705882355^2 - 16)/(2 * 5.1911764705882355^1) = 4.136664722546242

n = 2, value = 16, guess = 4.136664722546242
   abs(guess^n - value) = abs(4.136664722546242^2 - 16) = 1.1119950267585779
   guess_new = guess - (guess^n - value)/(n * guess^(n-1))
   guess_new = 4.136664722546242 - (4.136664722546242^2 - 16)/(2 * 4.136664722546242^1) = 4.002257524798522

n = 2, value = 16, guess = 4.002257524798522
   abs(guess^n - value) = abs(4.002257524798522^2 - 16) = 0.018065294806394405
   guess_new = guess - (guess^n - value)/(n * guess^(n-1))
   guess_new = 4.002257524798522 - (4.002257524798522^2 - 16)/(2 * 4.002257524798522^1) = 4.000000636692939

Result: 4.000000636692939
Verification: 4.000000636692939^2 = 16.00000509354392

Testing the Prototype (2)

print("Cube root of 27 (n=3, value=27):")
result = newtons_nth_root(3, 27)
print(f"Result: {result}")
print(f"Verification: {result}^3 = {result**3}\n")

Cube root of 27 (n=3, value=27):
n = 3, value = 27, guess = 1.0
   abs(guess^n - value) = abs(1.0^3 - 27) = 26.0
   guess_new = guess - (guess^n - value)/(n * guess^(n-1))
   guess_new = 1.0 - (1.0^3 - 27)/(3 * 1.0^2) = 9.666666666666666

n = 3, value = 27, guess = 9.666666666666666
   abs(guess^n - value) = abs(9.666666666666666^3 - 27) = 876.2962962962961
   guess_new = guess - (guess^n - value)/(n * guess^(n-1))
   guess_new = 9.666666666666666 - (9.666666666666666^3 - 27)/(3 * 9.666666666666666^2) = 6.540758356453956

n = 3, value = 27, guess = 6.540758356453956
   abs(guess^n - value) = abs(6.540758356453956^3 - 27) = 252.82358364070478
   guess_new = guess - (guess^n - value)/(n * guess^(n-1))
   guess_new = 6.540758356453956 - (6.540758356453956^3 - 27)/(3 * 6.540758356453956^2) = 4.570876778578707

n = 3, value = 27, guess = 4.570876778578707
   abs(guess^n - value) = abs(4.570876778578707^3 - 27) = 68.49893783892396
   guess_new = guess - (guess^n - value)/(n * guess^(n-1))
   guess_new = 4.570876778578707 - (4.570876778578707^3 - 27)/(3 * 4.570876778578707^2) = 3.4780192333867963

n = 3, value = 27, guess = 3.4780192333867963
   abs(guess^n - value) = abs(3.4780192333867963^3 - 27) = 15.07226932492673
   guess_new = guess - (guess^n - value)/(n * guess^(n-1))
   guess_new = 3.4780192333867963 - (3.4780192333867963^3 - 27)/(3 * 3.4780192333867963^2) = 3.0626891086275365

n = 3, value = 27, guess = 3.0626891086275365
   abs(guess^n - value) = abs(3.0626891086275365^3 - 27) = 1.728221615462001
   guess_new = guess - (guess^n - value)/(n * guess^(n-1))
   guess_new = 3.0626891086275365 - (3.0626891086275365^3 - 27)/(3 * 3.0626891086275365^2) = 3.0012744065061754

n = 3, value = 27, guess = 3.0012744065061754
   abs(guess^n - value) = abs(3.0012744065061754^3 - 27) = 0.03442359474400192
   guess_new = guess - (guess^n - value)/(n * guess^(n-1))
   guess_new = 3.0012744065061754 - (3.0012744065061754^3 - 27)/(3 * 3.0012744065061754^2) = 3.0000005410641766

Result: 3.0000005410641766
Verification: 3.0000005410641766^3 = 27.000014608735402

Testing the Prototype (3)

print("Fourth root of 81 (n=4, value=81):")
result = newtons_nth_root(4, 81)
print(f"Result: {result}")
print(f"Verification: {result}^4 = {result**4}\n")

Fourth root of 81 (n=4, value=81):
n = 4, value = 81, guess = 1.0
   abs(guess^n - value) = abs(1.0^4 - 81) = 80.0
   guess_new = guess - (guess^n - value)/(n * guess^(n-1))
   guess_new = 1.0 - (1.0^4 - 81)/(4 * 1.0^3) = 21.0

n = 4, value = 81, guess = 21.0
   abs(guess^n - value) = abs(21.0^4 - 81) = 194400.0
   guess_new = guess - (guess^n - value)/(n * guess^(n-1))
   guess_new = 21.0 - (21.0^4 - 81)/(4 * 21.0^3) = 15.752186588921283

n = 4, value = 81, guess = 15.752186588921283
   abs(guess^n - value) = abs(15.752186588921283^4 - 81) = 61488.18289808421
   guess_new = guess - (guess^n - value)/(n * guess^(n-1))
   guess_new = 15.752186588921283 - (15.752186588921283^4 - 81)/(4 * 15.752186588921283^3) = 11.81932080918686

n = 4, value = 81, guess = 11.81932080918686
   abs(guess^n - value) = abs(11.81932080918686^4 - 81) = 19434.068636062897
   guess_new = guess - (guess^n - value)/(n * guess^(n-1))
   guess_new = 11.81932080918686 - (11.81932080918686^4 - 81)/(4 * 11.81932080918686^3) = 8.876755039613878

n = 4, value = 81, guess = 8.876755039613878
   abs(guess^n - value) = abs(8.876755039613878^4 - 81) = 6127.932543617901
   guess_new = guess - (guess^n - value)/(n * guess^(n-1))
   guess_new = 8.876755039613878 - (8.876755039613878^4 - 81)/(4 * 8.876755039613878^3) = 6.686517196520891

n = 4, value = 81, guess = 6.686517196520891
   abs(guess^n - value) = abs(6.686517196520891^4 - 81) = 1917.9404828939596
   guess_new = guess - (guess^n - value)/(n * guess^(n-1))
   guess_new = 6.686517196520891 - (6.686517196520891^4 - 81)/(4 * 6.686517196520891^3) = 5.082624768192105

n = 4, value = 81, guess = 5.082624768192105
   abs(guess^n - value) = abs(5.082624768192105^4 - 81) = 586.3477398915912
   guess_new = guess - (guess^n - value)/(n * guess^(n-1))
   guess_new = 5.082624768192105 - (5.082624768192105^4 - 81)/(4 * 5.082624768192105^3) = 3.966195743486564

n = 4, value = 81, guess = 3.966195743486564
   abs(guess^n - value) = abs(3.966195743486564^4 - 81) = 166.45519543819964
   guess_new = guess - (guess^n - value)/(n * guess^(n-1))
   guess_new = 3.966195743486564 - (3.966195743486564^4 - 81)/(4 * 3.966195743486564^3) = 3.2992124877307853

n = 4, value = 81, guess = 3.2992124877307853
   abs(guess^n - value) = abs(3.2992124877307853^4 - 81) = 37.478937202150505
   guess_new = guess - (guess^n - value)/(n * guess^(n-1))
   guess_new = 3.2992124877307853 - (3.2992124877307853^4 - 81)/(4 * 3.2992124877307853^3) = 3.0382990701981023

n = 4, value = 81, guess = 3.0382990701981023
   abs(guess^n - value) = abs(3.0382990701981023^4 - 81) = 4.216184080510672
   guess_new = guess - (guess^n - value)/(n * guess^(n-1))
   guess_new = 3.0382990701981023 - (3.0382990701981023^4 - 81)/(4 * 3.0382990701981023^3) = 3.000718098021805

n = 4, value = 81, guess = 3.000718098021805
   abs(guess^n - value) = abs(3.000718098021805^4 - 81) = 0.07758243669628939
   guess_new = guess - (guess^n - value)/(n * guess^(n-1))
   guess_new = 3.000718098021805 - (3.000718098021805^4 - 81)/(4 * 3.000718098021805^3) = 3.000000257729561

Result: 3.000000257729561
Verification: 3.000000257729561^4 = 81.00002783479616

Testing the Prototype ((4)

print("4. Square root of 10 (n=2, value=10):")
result = newtons_nth_root(2, 10)
print(f"Result: {result}")
print(f"Verification: {result}^2 = {result**2}\n")

4. Square root of 10 (n=2, value=10):
n = 2, value = 10, guess = 1.0
   abs(guess^n - value) = abs(1.0^2 - 10) = 9.0
   guess_new = guess - (guess^n - value)/(n * guess^(n-1))
   guess_new = 1.0 - (1.0^2 - 10)/(2 * 1.0^1) = 5.5

n = 2, value = 10, guess = 5.5
   abs(guess^n - value) = abs(5.5^2 - 10) = 20.25
   guess_new = guess - (guess^n - value)/(n * guess^(n-1))
   guess_new = 5.5 - (5.5^2 - 10)/(2 * 5.5^1) = 3.659090909090909

n = 2, value = 10, guess = 3.659090909090909
   abs(guess^n - value) = abs(3.659090909090909^2 - 10) = 3.3889462809917354
   guess_new = guess - (guess^n - value)/(n * guess^(n-1))
   guess_new = 3.659090909090909 - (3.659090909090909^2 - 10)/(2 * 3.659090909090909^1) = 3.196005081874647

n = 2, value = 10, guess = 3.196005081874647
   abs(guess^n - value) = abs(3.196005081874647^2 - 10) = 0.21444848336856914
   guess_new = guess - (guess^n - value)/(n * guess^(n-1))
   guess_new = 3.196005081874647 - (3.196005081874647^2 - 10)/(2 * 3.196005081874647^1) = 3.1624556228038903

n = 2, value = 10, guess = 3.1624556228038903
   abs(guess^n - value) = abs(3.1624556228038903^2 - 10) = 0.0011255662039406644
   guess_new = guess - (guess^n - value)/(n * guess^(n-1))
   guess_new = 3.1624556228038903 - (3.1624556228038903^2 - 10)/(2 * 3.1624556228038903^1) = 3.162277665175675

Result: 3.162277665175675
Verification: 3.162277665175675^2 = 10.000000031668918

Challenge!

Can you modify the newtons_cube_root() algorithm to find the forth root newtons_4_root()

 

Hint: Use the general case to create the code.